8.4_裁剪替代目标函数可视化

别担心，如果现在这个概念对你来说还有些难以理解是很正常的。接下来，我们将看一下这个裁剪替代目标函数的真实面目，这将有助于更好地理解其作用。

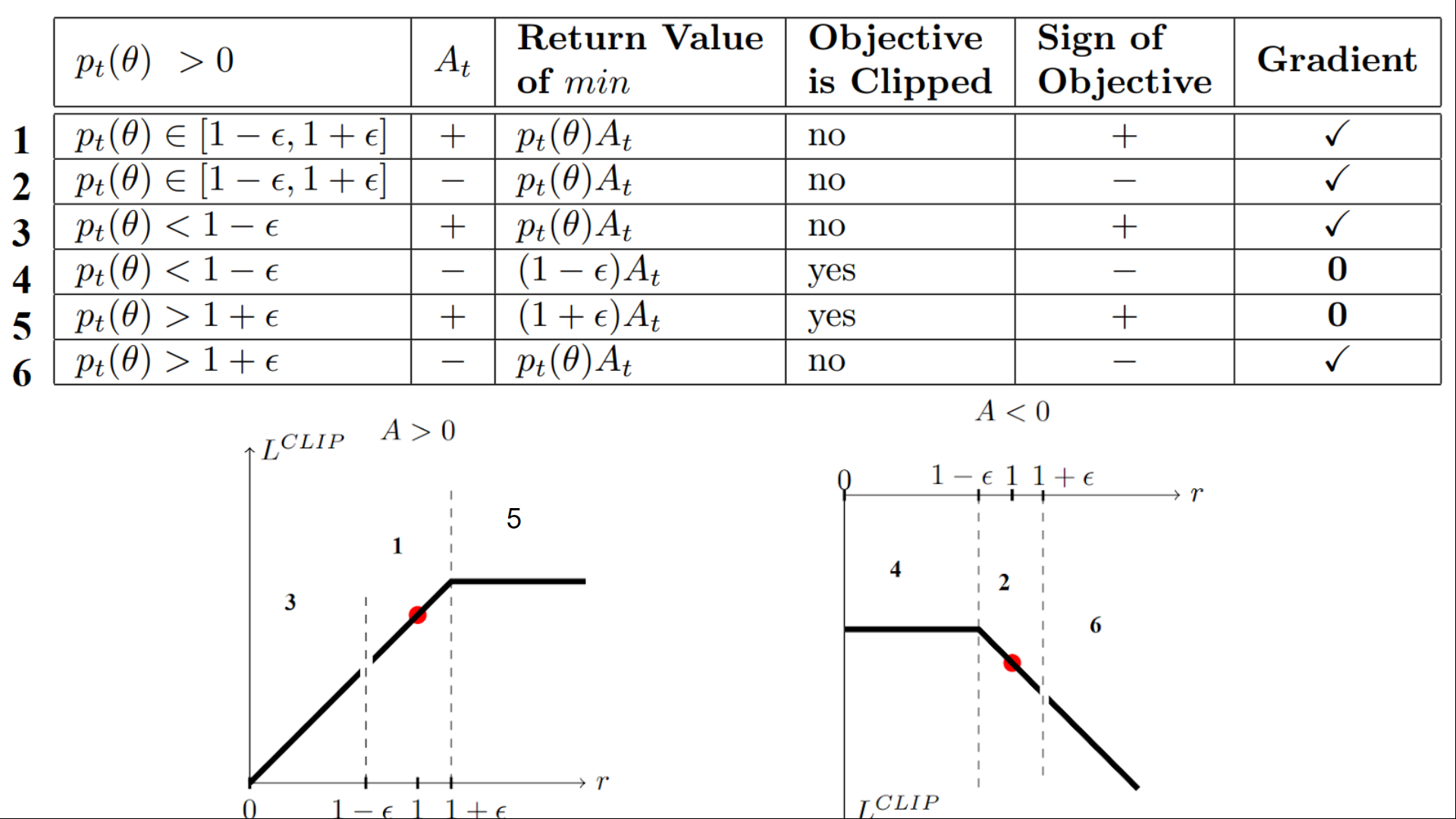
我们有六种不同的情况。首先要记住的是，我们在裁剪和未裁剪目标之间取最小值。

情况 1 和 2 ：比率在范围内

在情况 1 和 2 中，裁剪不适用，因为比率在范围内 \( [1 - \epsilon, 1 + \epsilon] \)

在情况 1 中，我们有一个正向优势：该动作比该状态下所有动作的平均水平都要好。因此，我们应该鼓励当前策略增加在该状态下采取该动作的概率。

由于比率在区间之间，我们可以增加策略在该状态下采取该动作的概率。

在情况 2 中，我们有一个负向优势：该动作比该状态下所有动作的平均水平都要差。因此，我们应该阻止当前策略在该状态下采取该动作。

由于比率在区间之间，我们可以减少策略在该状态下采取该动作的概率。

如果概率比率低于 \( [1 - \epsilon] \)，则在该状态下采取该动作的概率远低于旧策略。

如果，如情况 3，优势估计为正（A>0），则你希望增加在该状态下采取该动作的概率。

但是，如果像情况 4 一样，优势估计为负，我们不希望进一步减少在该状态下采取该动作的概率。因此，梯度 = 0（因为我们处于平直的线上），所以我们不更新权重。

如果概率比率高于 \( [1 + \epsilon] \)，那么当前策略在该状态下采取该动作的概率比以前的策略要高得多。

如果像情况 5 一样，优势是正的，那么我们不想太贪心。我们已经比以前的策略更有可能在该状态下采取该行动。因此，梯度等于 0（因为我们在平坦线上），我们不更新权重。

如果像情况 6 一样，优势是负的，我们想要减少在该状态下采取该行动的概率。

因此，如果我们总结一下，我们只使用未裁剪目标部分来更新策略。当最小值为裁剪目标部分时，我们不会更新策略权重，因为梯度将等于 0。

因此，我们仅在以下情况下更新策略：

**你可能会想知道为什么当最小值是裁剪比率时，梯度会为 0。在这种情况下，当比率被裁剪时，其导数将不是 \( r_t(\theta) * A_t \) 的导数，而是 \( (1-\epsilon) A_t\) 或 \( (1+\epsilon) A_t\) 的导数，这两者都等于 0。

总结一下，多亏了裁剪替代目标函数，我们限制了当前策略与旧策略之间的变化范围。因为我们消除了让概率比率移动到区间之外的激励，这个裁剪对梯度有影响。如果比率大于 \( 1+\epsilon \) 或小于 \( 1-\epsilon \)，梯度将等于 0。

PPO 演员-评论员风格的最终裁剪替代目标函数损失看起来像这样，它是裁剪替代目标函数、价值损失函数和熵奖励的组合：

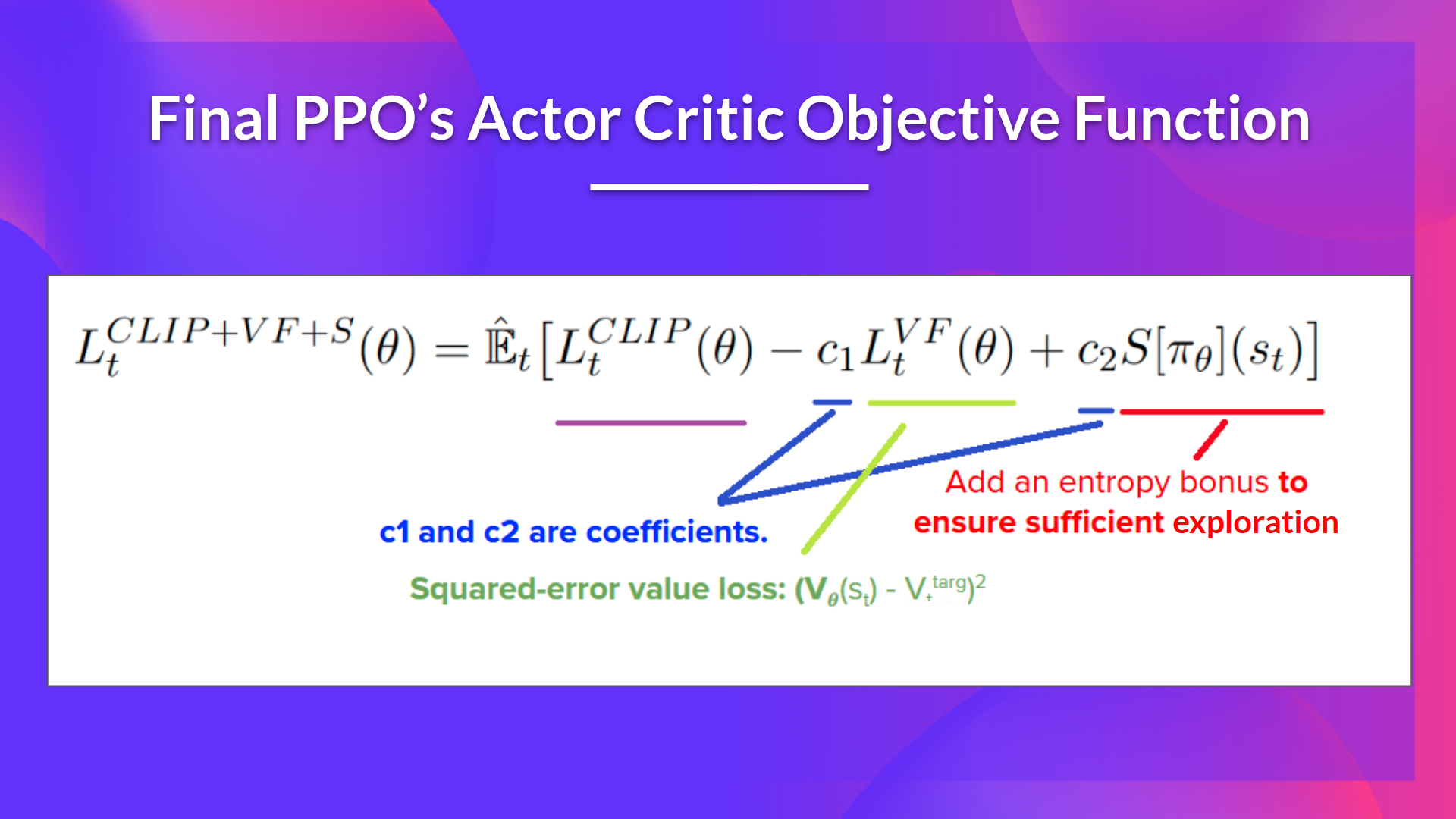
这是一个相当复杂的概念。请仔细查看表格和图表以理解这些情况。你必须理解为什么这个方法可以运行。 如果想要更深入了解，最好的资源是 Daniel Bick 的文章为近端策略优化提供连贯的独立解释，特别是第3.4部分。