6.3_优势演员--评论员（A2C）方法

使用演员--评论员方法减少方差

减少强化学习算法的方差并更快更好地训练我们的智能体的解决方案是结合使用基于策略和基于价值的方法：演员--评论员方法。

要了解演员--评论员方法，请想象你玩电子游戏。 你可以和一个朋友一起玩，他会给你一些反馈。 此种情况下，你是演员，你的朋友是评论员。

一开始你不知道怎么玩，所以你随机尝试一些动作。 评论员会观察你的行为并提供反馈。

从此反馈中学习，你将更新你的策略并更好地玩该游戏。

另一方面，你的朋友（评论员）也会更新他们提供反馈的方式，以便下次可以做得更好。

这就是“演员--评论员”方法背后的理念。我们学习了两个函数近似:

• 一项策略，控制我们的智能体如何行动: \( \pi_{\theta}(s,a) \)
• 一个价值函数，通过衡量所采取的行动有多好来协助策略更新: \( \hat{q}_{w}(s,a) \)

演员--评论员方法过程

现在我们已经有了对演员--评论员方法的总体看法，让我们更深入地了解演员和评论员在训练过程中是如何一起改进的。

正如我们所见，对于演员--评论员方法，有两个函数近似（两个神经网络）：

• 演员，一个参数化的策略函数 theta: \( \pi_{\theta}(s,a) \)
• 评论员，一个参数化的价值函数 w: \( \hat{q}_{w}(s,a) \)

让我们看看训练过程，了解 演员 和 评论员 是如何优化的：

• 在每个时间步长 t，我们从环境中得到当前状态 \( S_t\) 并将其通过我们的演员和评论员作为输入传递。
• 我们的训练策略接收状态并输出一个动作 \( A_t \)。

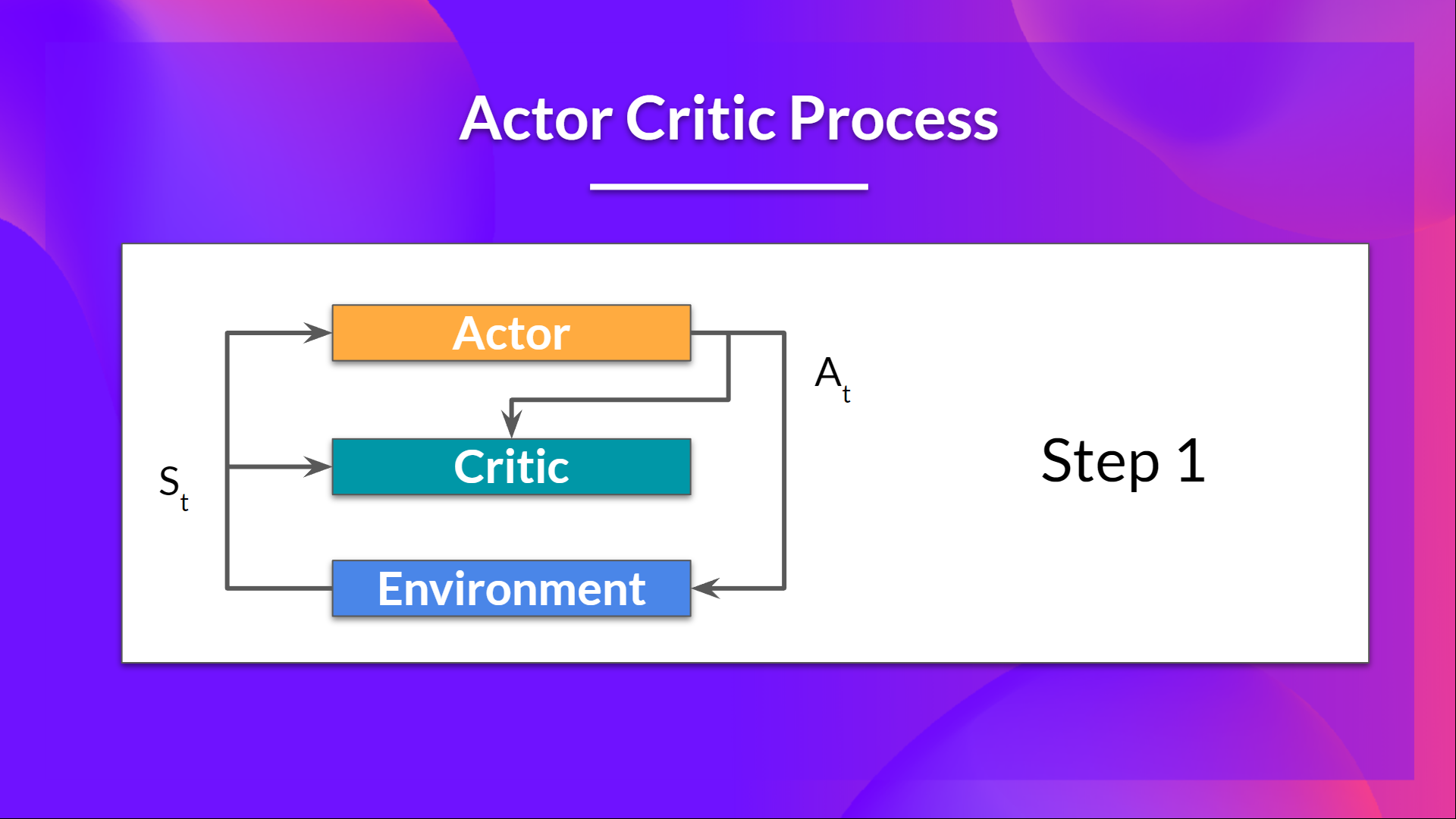
• 评论员也将该动作作为输入，并使用 \( S_t\) 和 \( A_t \)，计算在该状态下采取该动作的值：Q 值。

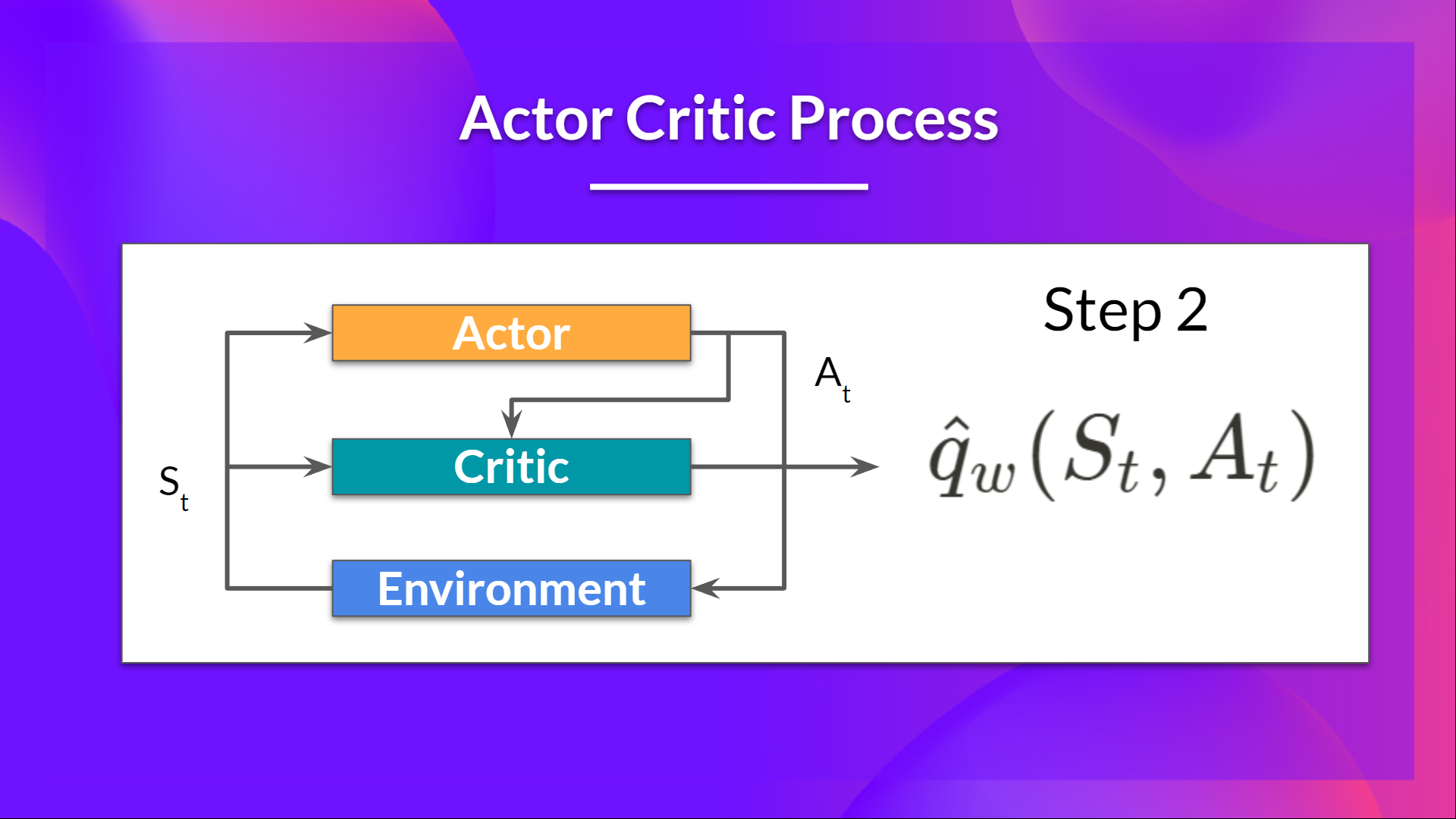
• 在环境中执行的动作 \( A_t\) 输出一个新状态 \( S_{t+1}\) 和一个奖励 \( R_{t+1} \) 。

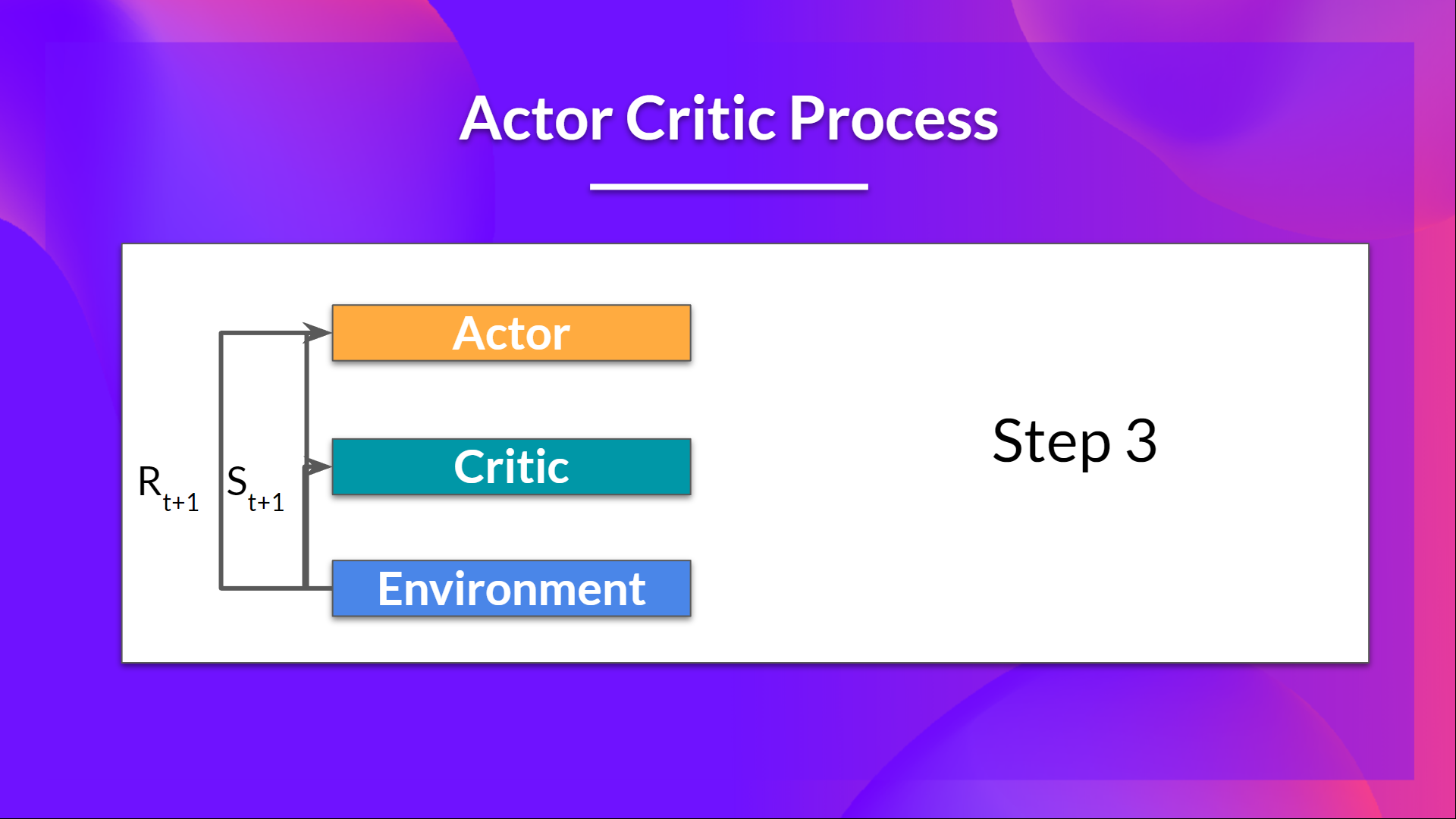
• 演员使用 Q 值更新其策略参数。

• 由于其更新的参数，在给定新状态 \( S_{t+1} \) 的情况下，Actor 会在 \( A_{t+1} \) 处产生要采取的下一个动作。
• 然后评论员更新它的参数的值。

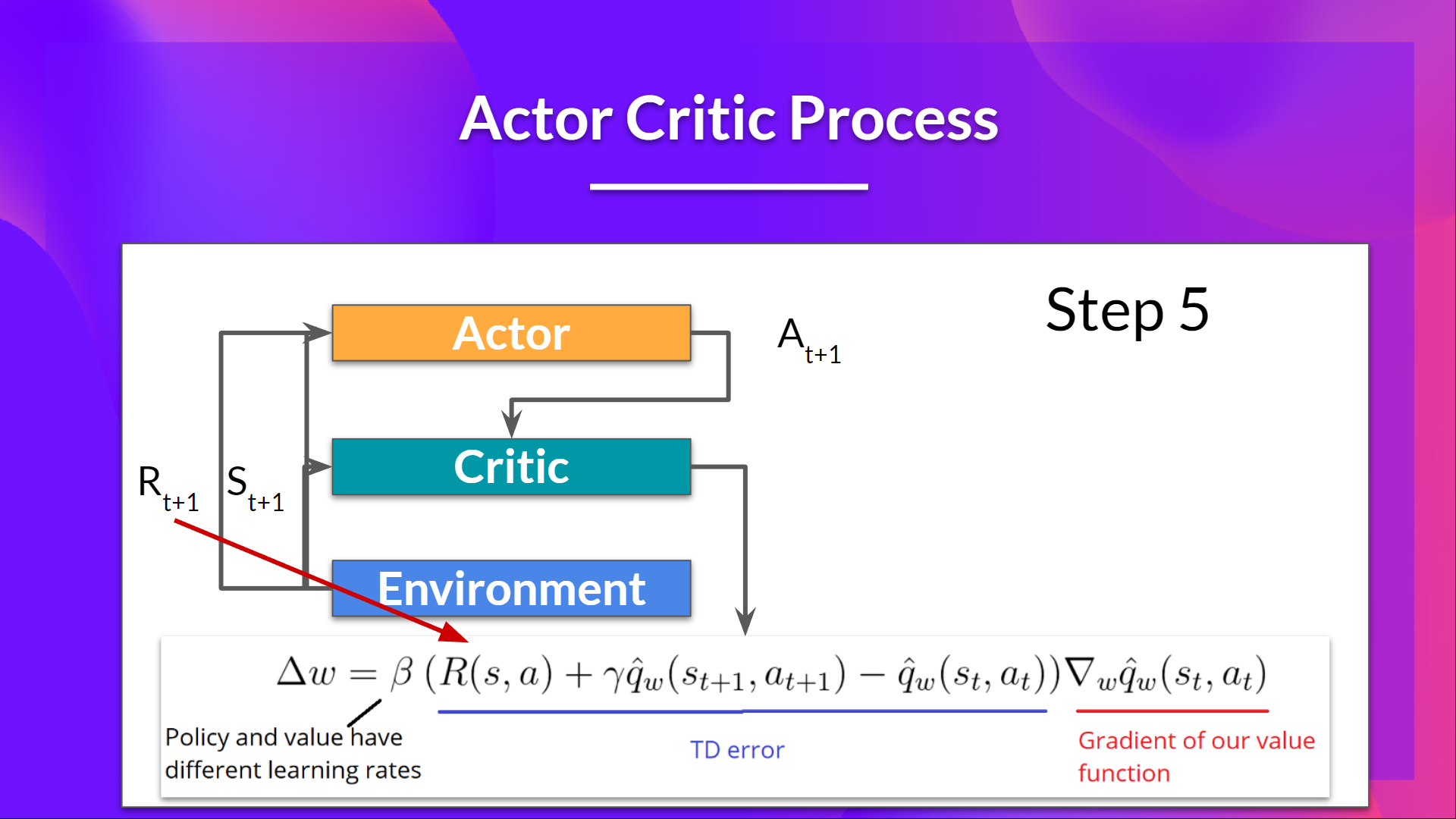
在 A2C 中增加优势

我们可以通过使用优势函数作为评论员以替代动作价值函数来进一步稳定学习。

这个想法是优势函数计算一个动作与一个状态下可能的其他动作相比的相对优势：与状态的平均值相比，在一个状态下采取该动作如何更好。 它是从状态动作对中减去状态的平均值：

换句话说，这个函数计算如果我们在那个状态下采取这个行动，我们得到的额外奖励和我们在那个状态下得到的平均奖励相比较的结果。

额外的奖励是超出该状态期望价值的东西。

• 如果 A(s,a) > 0: 我们的梯度被推向那个方向。
• 如果 A(s,a) < 0 （我们的动作确实比那个状态的平均值差），我们的梯度被推向相反的方向。

实现这个优势函数的问题在于它需要两个值函数——\( Q(s,a)\) 和 \( V(s)\)。 幸运的是，我们可以使用 TD 误差作为优势函数的较好估计量。