6.2_Reinforce 中的方差问题

在 Reinforce 中，我们想要根据回报的高低来成比例地增加轨迹中动作的概率。

回报 \(R(\tau)\) 是使用蒙特卡洛采样计算的。我们收集轨迹并计算折扣回报，并使用该分数来增加或减少在该轨迹中采取的每个动作的概率。如果回报较好，所有动作都将通过增加采取动作的可能性来“加强”。

\(R(\tau) = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ...\)

这种方法的优点是它是无偏的，由于我们没有估算回报，因此我们仅使用我们获得的真实回报。

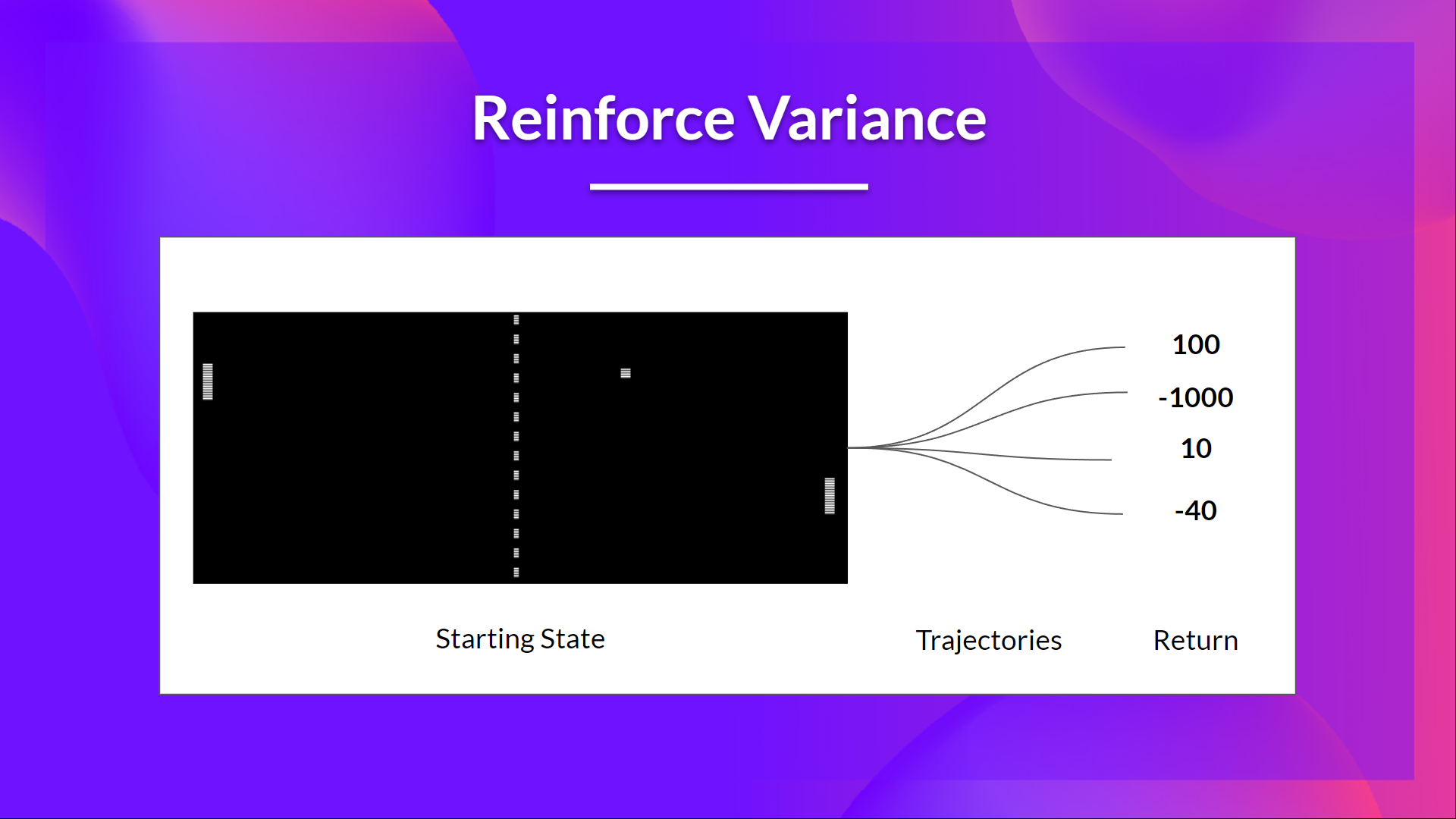
鉴于环境的随机性(回合中的随机事件)和策略的随机性，**轨迹可能导致不同的回报，这可能导致高方差。**因此，相同的起始状态可能导致非常不同的回报。
正因为如此，从同一状态开始的回报在不同的回合之间可能会有很大的不同。

解决方案是通过使用大量轨迹来减轻方差，希望在任何一个轨迹中引入的方差将总体减少，并提供对回报的“真实”估计。

然而，增加批量大小会明显降低样本效率。所以我们需要找到额外的机制来减少方差。

如果你想更深入地研究深度强化学习中的方差和偏差权衡问题，你可以查看这两篇文章：