4.4_深入了解策略梯度方法
了解全局
我们刚刚了解到策略梯度方法旨在找到参数 \( \theta \) 即最大化期望回报。
这个想法是我们有一个参数化的随机策略。在我们的例子中,神经网络输出动作的概率分布。采取每个动作的概率也称为动作偏好。
以 CartPole-v1 为例:
- 作为输入,我们有一个状态。
- 作为输出,我们有该状态下动作的概率分布。
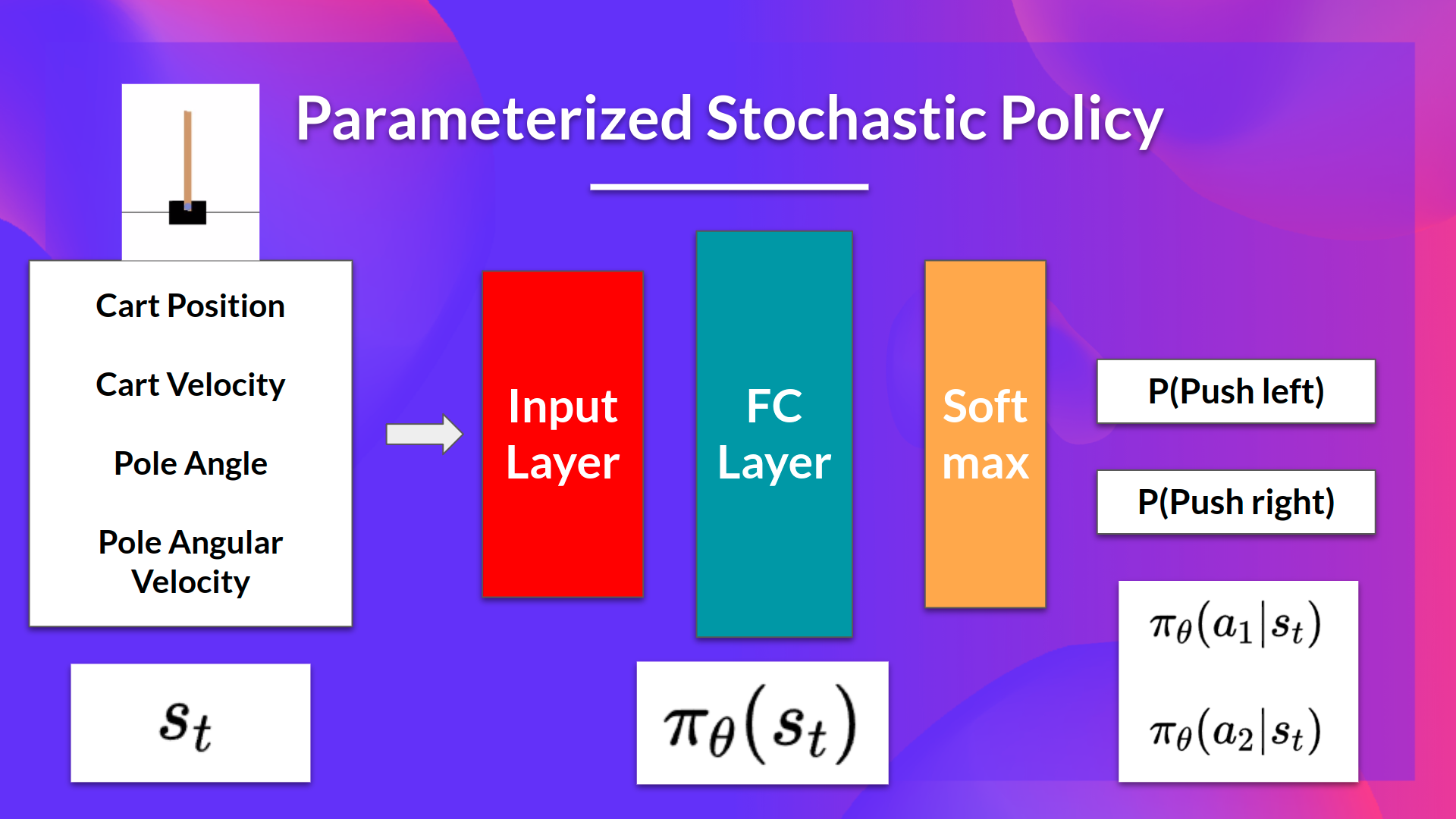
我们使用策略梯度的目标是通过调整策略来控制动作的概率分布,以便在未来更频繁地对好的动作(最大化回报)进行采样。 每次智能体与环境交互时,我们都会调整参数,以便将来更有可能对好的动作进行采样。
但是我们如何使用期望回报来优化权重呢?
一个想法是让智能体在一个完整的回合中进行交互。如果我们在这个回合获胜,我们就认为每个采取的动作都是好的,将来必须更多地采样它们,因为它们导致了胜利。
所以对于每个状态-动作对,我们想增加 \(P(a|s)\):在那个状态下采取那个动作的概率。如果输了就减少此概率。
策略梯度算法(简化)如下所示:

现在我们了解了全局,让我们更深入地了解策略梯度方法。
深入了解策略梯度方法
我们有我们的随机策略 \(\pi\) ,该策略有一个参数 (\theta\)。这个 \(\pi\),给定一个状态,会输出动作的概率分布。

其中,\(\pi_\theta(a_t|s_t)\) 是智能体根据策略从状态 \(s_t\) 选择动作 \(a_t\) 的概率。
**但是我们怎么知道我们的策略是否好呢?**我们需要有一种方法来衡量它。要知道这一点,我们定义了一个分数/目标函数,称为 \(J(\theta)\)。
目标函数
在这里,目标函数给出了一个轨迹(不考虑奖励的状态动作序列(与一个回合相反))的智能体表现,并输出期望累积奖励。

让我们更详细地说明这个公式:
- 期望回报(也称为期望累积奖励)是所有可能的回报值 \(R(\tau)\) 的加权平均值(权重由 \(P(\tau;\theta)\) 给出)。

- \(R(\tau)\) : 这是一条任意轨迹的回报。为了使用它来计算期望回报,我们需要将其乘以每个可能轨迹的概率。
- \(P(\tau;\theta)\) : 每个可能轨迹 \(\tau\) 的概率(该概率取决于 \(\theta\),因为它定义了用于选择轨迹动作的策略,这影响了所访问的状态)。

- \(J(\theta)\) : 期望回报,我们通过对所有轨迹进行求和来计算它,其中包括给定 \(\theta \) 下采取该轨迹的概率以及该轨迹的回报。
我们的目标是通过找到能够输出最佳动作概率分布的 \(\theta\) 来最大化期望累积奖励。

梯度上升和策略梯度定理
策略梯度是一个优化问题:我们想要找到最大化我们的目标函数 \(J(\theta)\) 的 \(\theta\) 值,因此我们需要使用 梯度上升。它是 梯度下降 的反向,因为它给出了 \(J(\theta)\) 最陡增加的方向。
(如果您需要关于梯度下降和梯度上升之间的区别的提醒,请参阅这个和这个)
我们的梯度上升更新步骤是:
\( \theta \leftarrow \theta + \alpha * \nabla_\theta J(\theta) \)
我们可以反复应用此更新状态,希望 \(\theta\) 收敛到最大化 \(J(\theta)\) 的值。
但是,我们有两个问题需要解决才能获得 \(J(\theta)\) 的导数:
-
我们无法计算出目标函数的真实梯度,因为这将意味着要计算每种可能轨迹的概率,这在计算上是非常昂贵的。因此我们希望通过采样估计(收集一些轨迹)来计算一个梯度估计。
-
我们还有另一个问题,我在下一个可选章节中详细介绍。为了对这个目标函数求导,我们需要对状态分布进行求导,这被称为马尔可夫决策过程动力学,它与环境相关。它给出了环境在给定当前状态和智能体采取的动作的情况下进入下一个状态的概率。问题是我们可能不知道它,因此无法对它进行求导。

幸运的是,我们将使用一种称为策略梯度定理的解决方案,它将帮助我们将目标函数重新表述为一个不涉及状态分布微分的可微分函数。

如果你想了解我们如何推导我们将用于近似梯度的这个公式,请查看下一个(可选)部分。
强化算法 (蒙特卡洛强化)
强化算法, 也叫做蒙特卡洛策略梯度, 是一种策略梯度算法,它使用来自整个回合的估计回报来更新策略参数 \(\theta\):
在一个循环中:
- 使用策略 \(\pi_\theta\) 收集一个轨迹 \(\tau\)
- 利用轨迹估算梯度 \(\hat{g} = \nabla_\theta J(\theta)\)
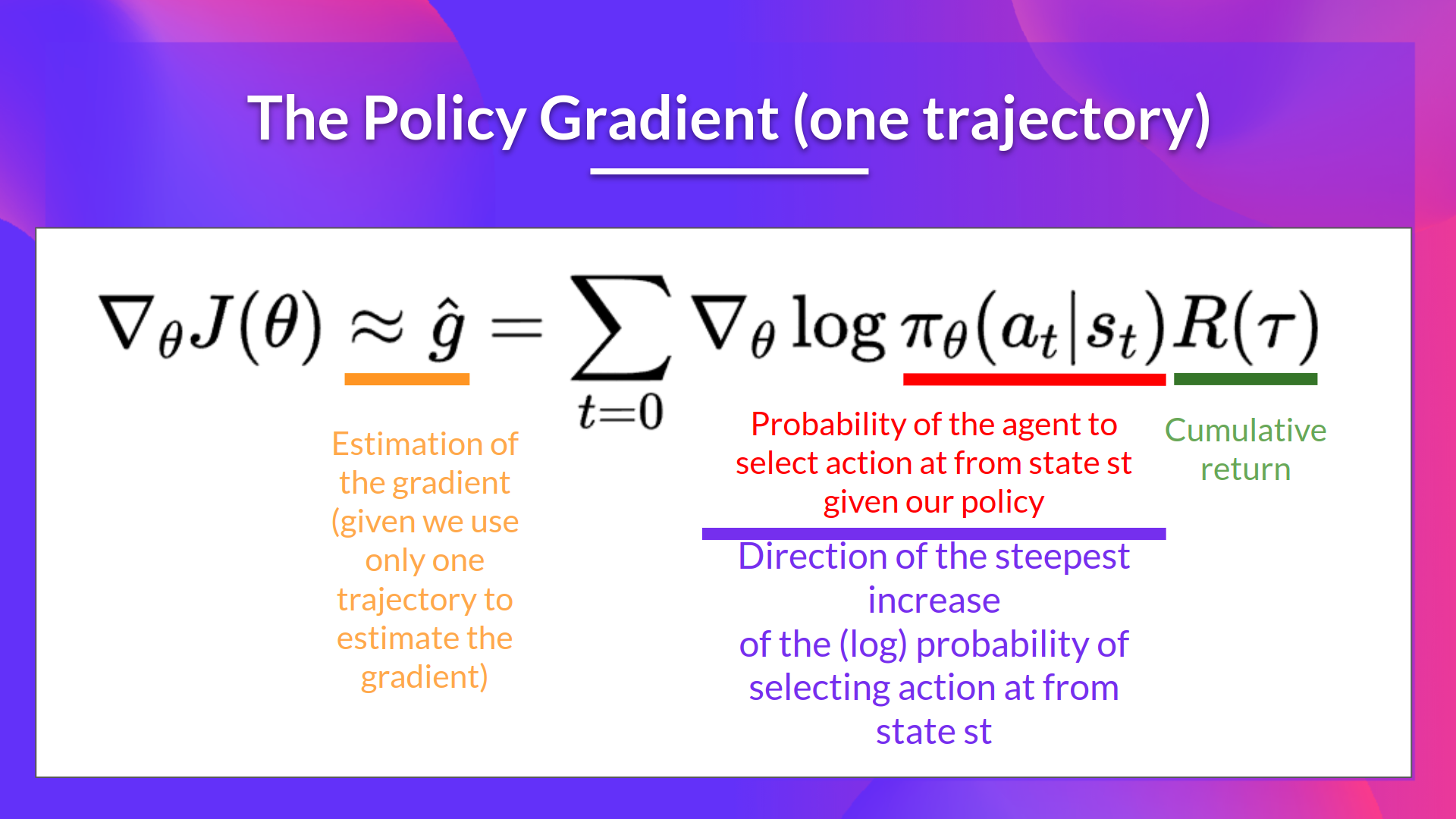
- 更新策略权重:\(\theta \leftarrow \theta + \alpha \hat{g}\)
我们可以做出以下解释:
- \(\nabla_\theta log \pi_\theta(a_t|s_t)\) 是选择从状态 \(s_t\) 选取动作 \(a_t\) 的 (log) 概率的最陡升高方向。它告诉我们:如果我们想要增加/减少在状态 \(s_t\) 选取动作 \(a_t\) 的对数概率,应该如何改变策略的权重。
- \(R(\tau)\) 是评分函数:
- 如果回报很高,它将提高(状态,动作)组合的概率。
- 反之,如果回报很低,它将降低(状态,动作)组合的概率。
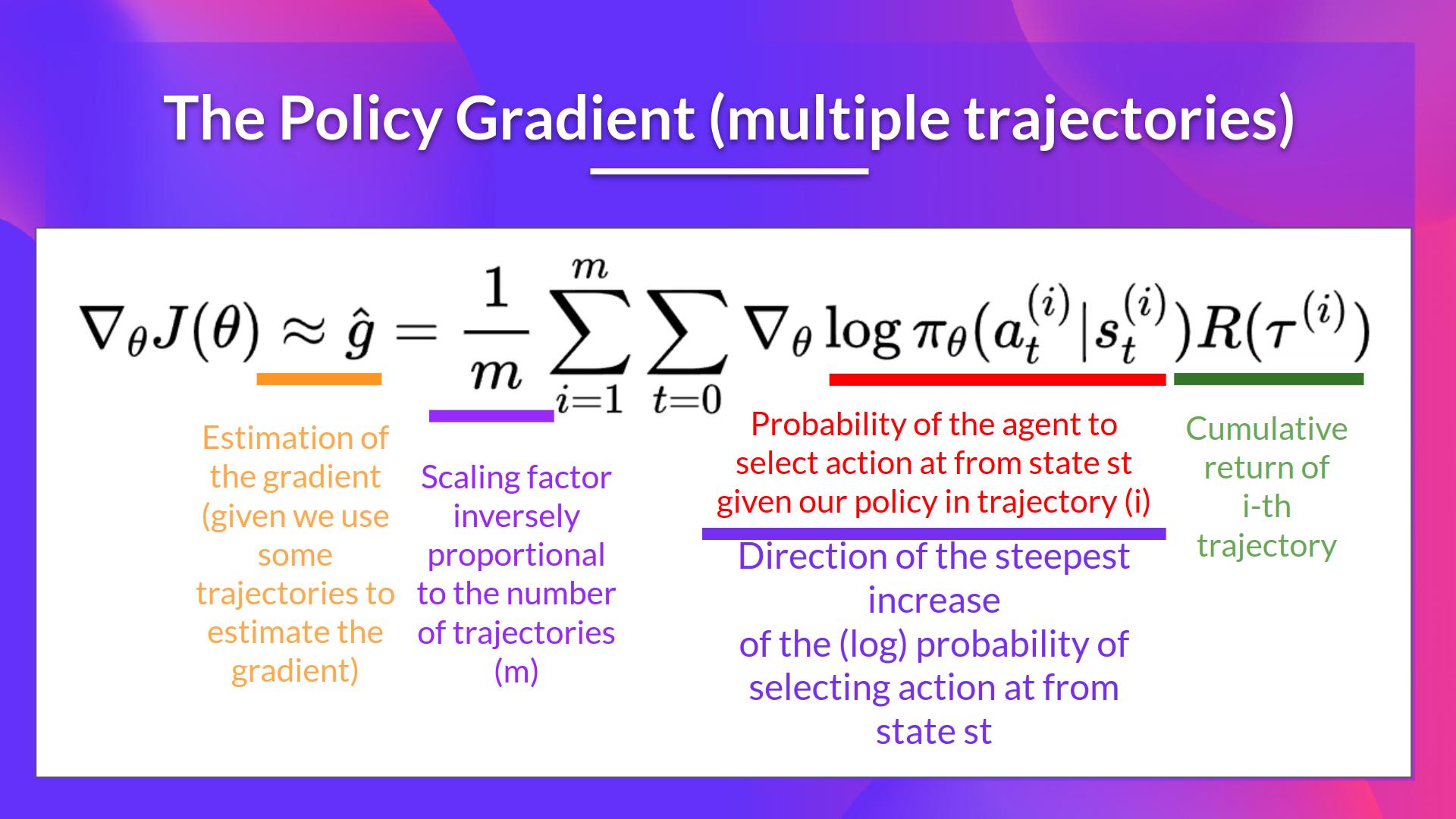
我们还可以**收集多个回合(轨迹)**来估计梯度: