4.3_策略梯度理论的优缺点

关于这点，你或许会问，“深度 Q-learning 已经棒极了！为什么还使用策略梯度理论？”。为了回答这个问题，让我们先学习一下策略梯度理论的优缺点。

优点

与基于价值的方法相比，它有很多优点。让我们看看其中的一些：

集成的简单性

我们可以直接估计策略而不存储额外的数据（动作值）。

策略梯度方法可以学习随机策略

策略梯度方法可以学习随机策略，而价值函数则不能。

这导致两个后果：

1. 我们不需要手动实现探索/利用权衡。由于我们输出动作的概率分布，因此智能体会探索状态空间而不总是采用相同的轨迹。
2. 我们也摆脱了感知混淆的问题。感知混淆是指两个状态看起来（或确实）相同但需要不同的动作。

让我们看一个例子：我们有一个智能真空吸尘器，它的目标是吸走灰尘，避免杀死仓鼠。

我们的真空吸尘器只能感知墙壁的位置。
问题在于，这两个位置的情况是具有感知混淆的状态，因为智能体对于每一个位置都感知到了上墙和下墙。

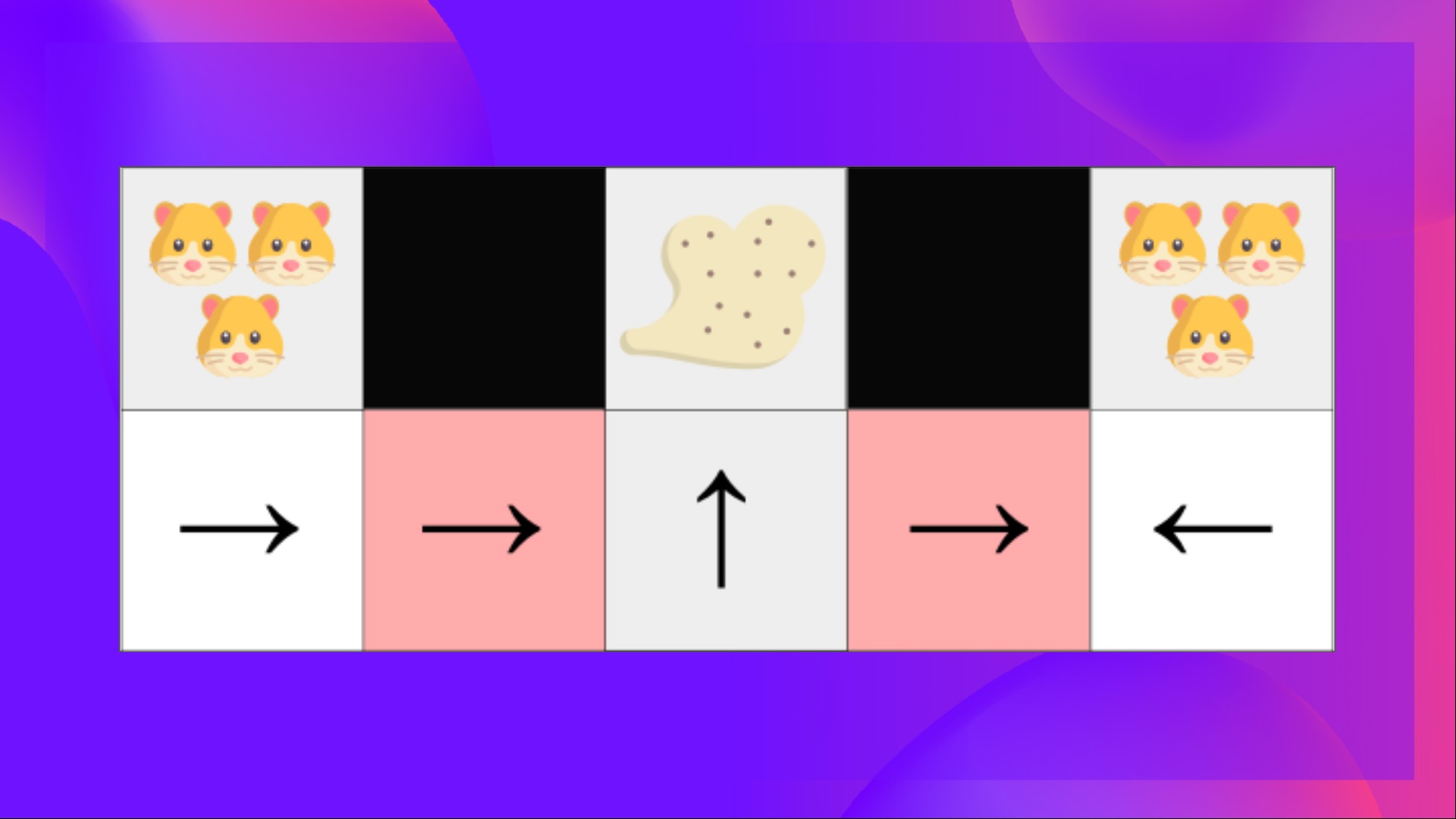
在确定性策略下，当处于红色状态时，策略要么向右移动，要么向左移动。这两种情况都会导致智能体陷入困境，无法清除灰尘。

在基于价值的强化学习算法下，我们学习了一种拟确定性策略（quasi-deterministic policy）（"贪心 epsilon 策略"）。因此，我们的智能体在找到灰尘之前可能需要花费很长时间。

另一方面，最优随机策略将在位置状态下随机向左或向右移动。因此，它不会被困住，有很高的概率到达目标状态。

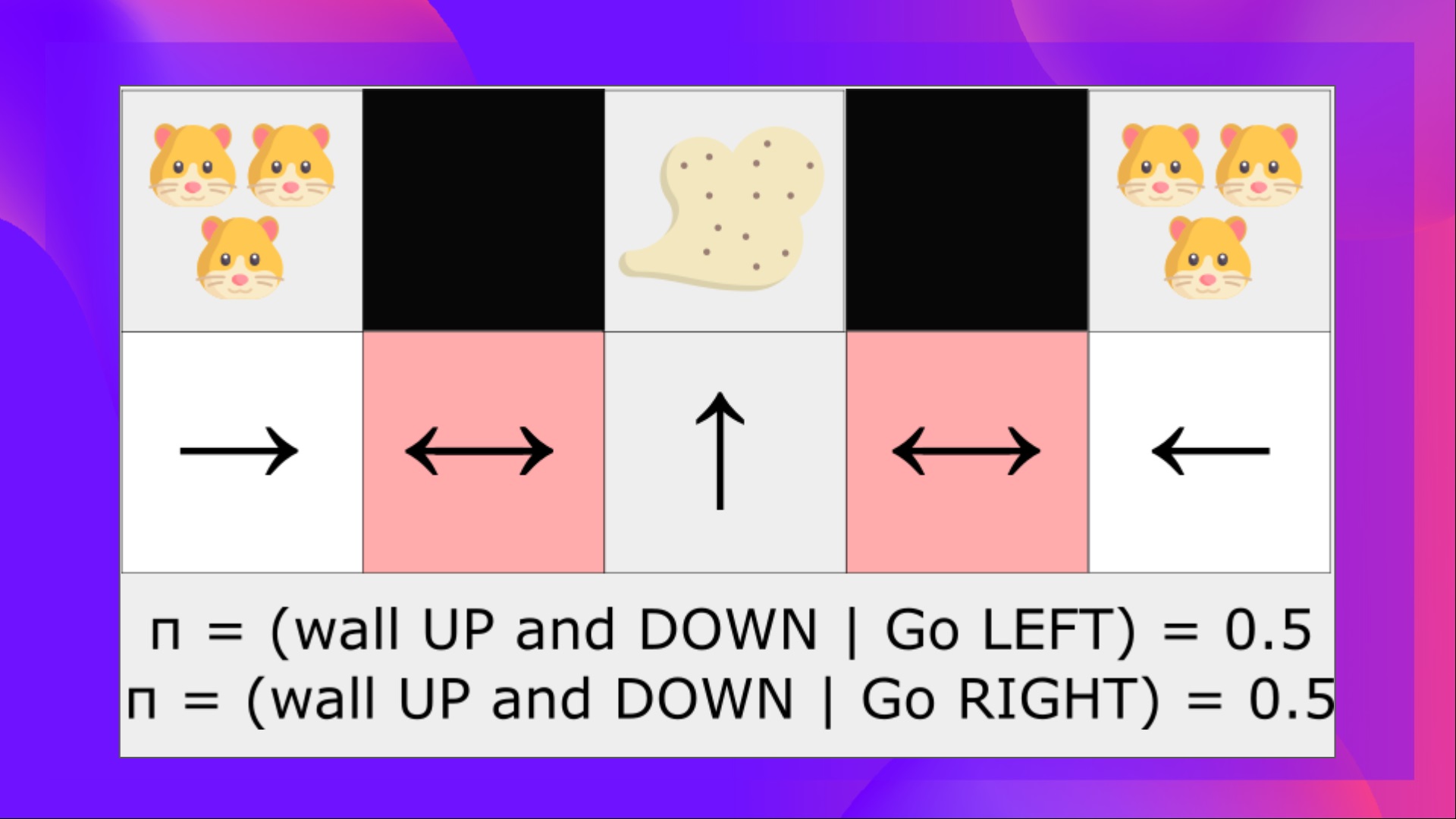
策略梯度方法在高维动作空间和连续动作空间中更有效

深度 Q 学习的问题在于，在给定当前状态的情况下，他们的预测会在每个时间步为每个可能的动作分配一个分数（最大预期未来奖励） 。

但是，如果我们有无限可能的动作呢？

例如，对于自动驾驶汽车，在每个状态下，你都可以（几乎）无限地选择动作（将方向盘转动 15°、17.2°、19.4°、鸣喇叭等）。我们需要为每个可能的动作输出一个 Q 值！而采取连续输出的最大动作本身就是一个优化问题！

相反，使用策略梯度方法，我们输出动作的概率分布。

策略梯度方法具有更好的收敛性

在基于价值的方法中，我们使用激进的操作来**改变价值函数：我们在 Q 估计上取最大值。**因此，如果动作估计值发生任意小的变化，导致具有最大值的动作不同，则动作概率可能会发生显著变化。

例如，如果在训练期间，最好的动作是向左移动（Q 值为 0.22），而在它之后的训练步骤是向右移动（因为右边的 Q 值变为 0.23），我们极大地改变了策略，因为现在策略将大部分时间都是向右移动而不是向左移动。

另一方面，在策略梯度方法中，随机策略行动偏好（采取行动的概率）随时间平稳变化。

缺点

当然，策略梯度方法也有一些缺点：

• 通常，策略梯度收敛于局部最大值而不是全局最优值。
• 策略梯度逐步变慢 ：训练可能需要更长的时间（效率低下）。
• 策略梯度可以有很高的方差。我们将在演员-评论员单元中看到为什么以及如何解决这个问题。

👉 如果您想更深入地了解策略梯度方法的优缺点, 你可以查看此视频.