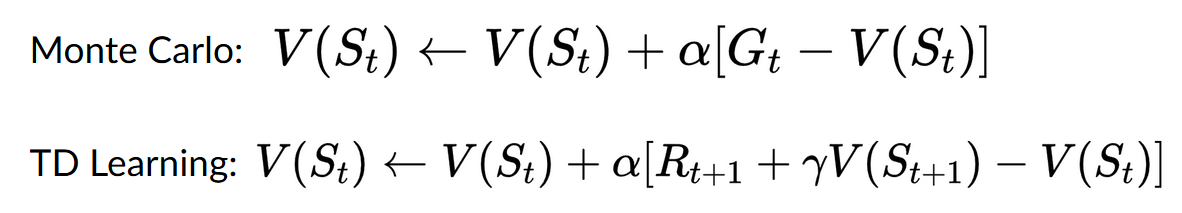2.4_蒙特卡洛 VS 时序差分学习

在深入学习Q-learning算法之前，我们需要先了解一下两种学习策略。

牢记智能体是通过与其环境交互来进行学习的，即给定经验和收到来自环境的奖励，智能体将更新其价值函数或策略。

蒙特卡洛和时序差分学习在训练价值函数或策略函数上是两种不同的策略，但他们都使用经验来解决强化学习问题。

蒙特卡洛在学习之前使用整个回合的经验；而时序差分则只使用一个步骤(S_t, A_t, R_{t+1}, S_{t+1})来进行学习。

我们将使用一个基于价值的方法案例来解释他们。

蒙特卡洛：在一个回合结束后进行学习

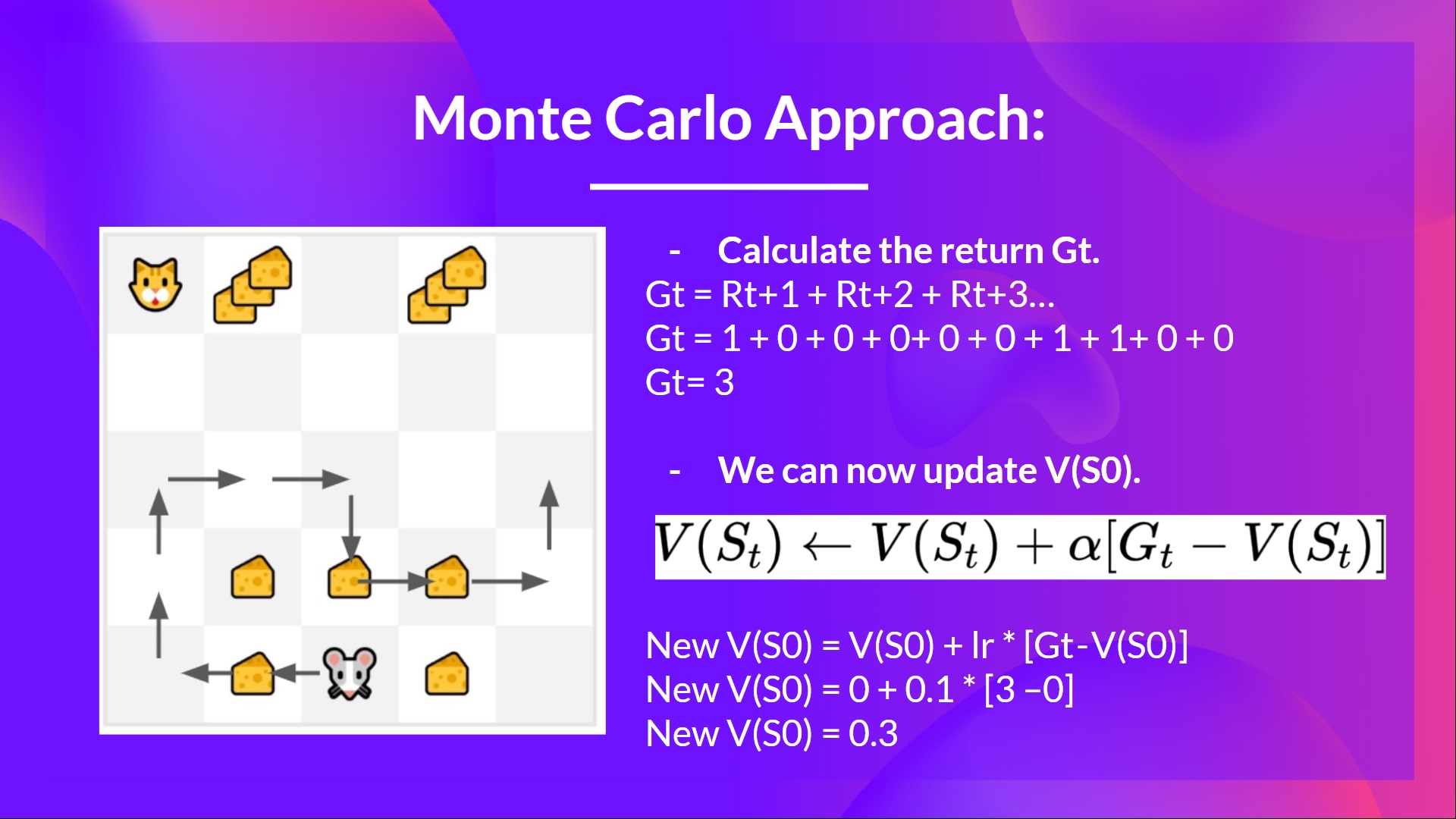
蒙特卡洛在回合结束时计算(G_t) (回报)并且使用其作为一个更新的目标(V(S_t))。

因此，在更新我们的价值函数之前，它需要一个完整的交互过程。

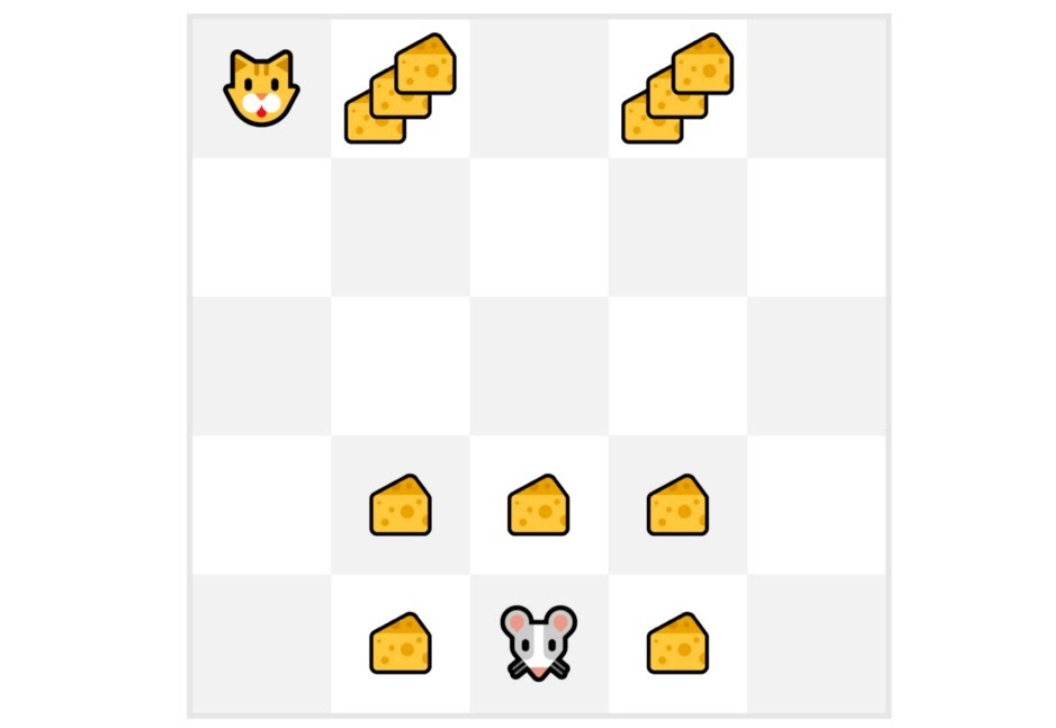
举个例子：

• 我们始终从相同的起点开始新的回合（episode）。

• 智能体根据策略（policy）选择行动。例如，使用一个 Epsilon Greedy 策略，该策略在探索（随机行动）和利用（利用之前经验）之间交替选择。

• 得到奖励（reward）和下一个状态（next state）。

• 如果猫吃掉老鼠或老鼠移动 > 10 步，则我们将终止该回合。

• 在该回合结束时，我们会得到一个状态、行动、奖励和下一个状态的元组列表。例如 [[状态为第三个瓷砖的底部，向左移动，+1，状态为第二个瓷砖的底部], [状态为第二个瓷砖的底部，向左移动，+0，状态为第一个瓷砖的底部]...]

• 智能体将计算总奖励 (G_t)（以衡量其性能）。

• 然后，它将基于以下公式更新 (V(s_t))。

  

• 最后以这些新知识来重新开始游戏

通过训练的回合越来越多，智能体会把游戏玩的越来越好。

例如，如果用蒙特卡洛训练了一个状态价值函数

• 我们刚刚开始训练值函数，所以它将为每个状态返回值0。

• 学习率（lr）为0.1，折扣率为1（没有折扣）。

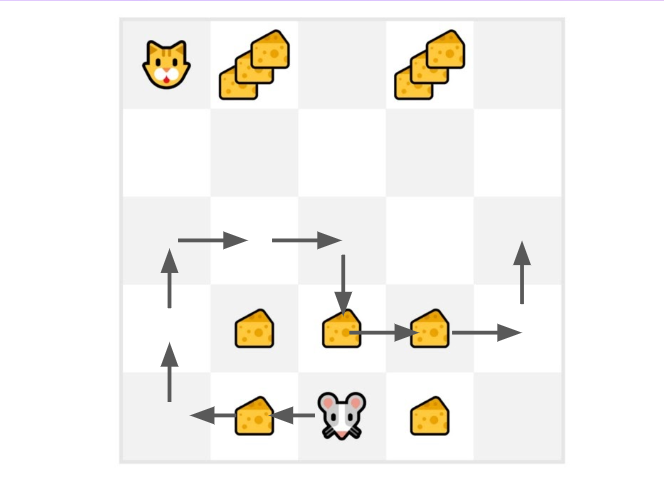
• 小老鼠将探索环境并采取随机动作。

  

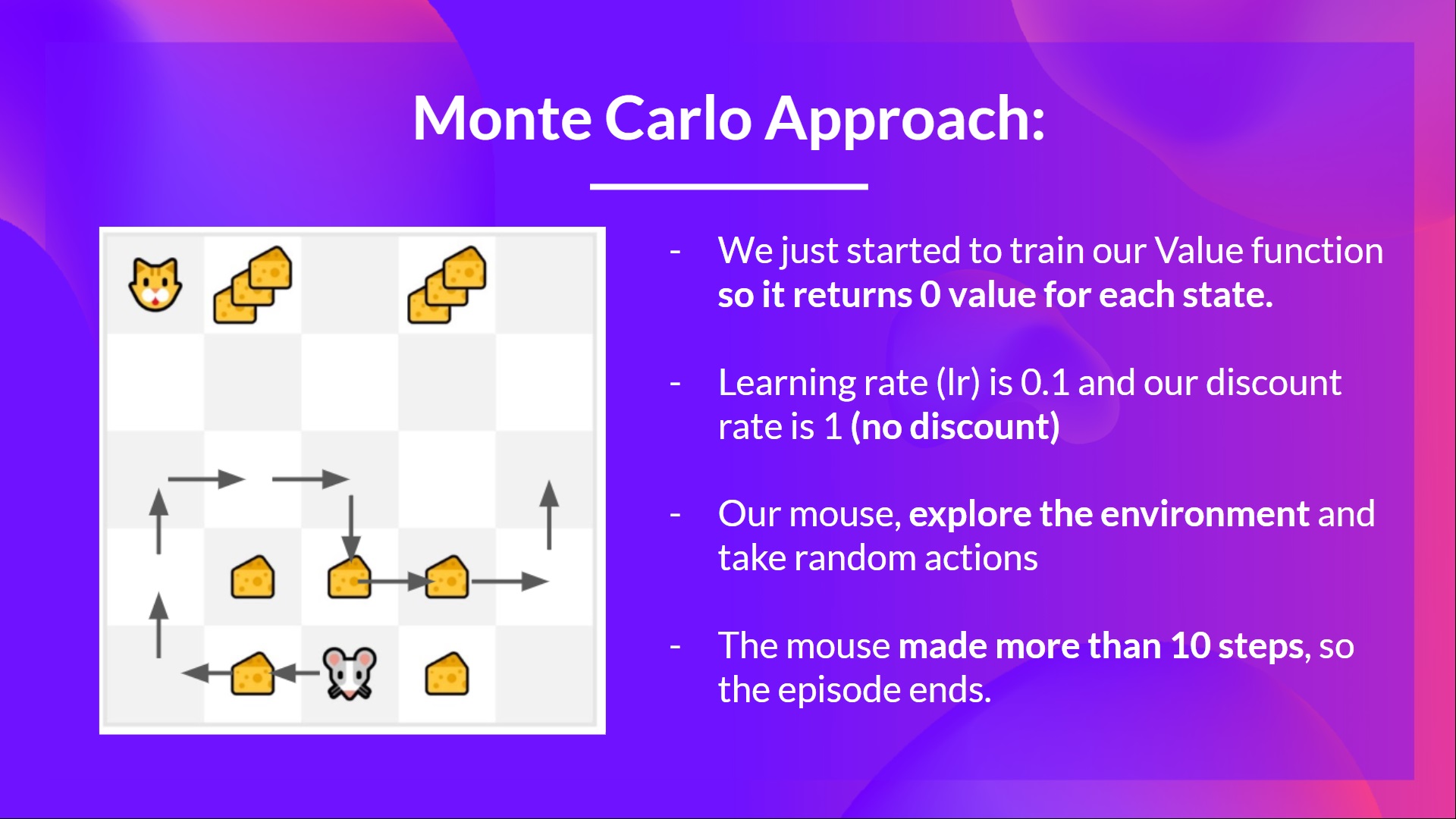
• 小老鼠的移动超过了十步，所以回合结束。

  

• 我们有一系列的状态、动作、奖励以及下一个状态，所以现在我们需要计算回报（G{t}）

• \(G_t = R_{t+1} + R_{t+2} + R_{t+3} ...\)

• \(G_t = R_{t+1} + R_{t+2} + R_{t+3}…\) (为简单起见，我们不对奖励进行折扣计算).

• \(G_t = 1 + 0 + 0 + 0+ 0 + 0 + 1 + 1 + 0 + 0\)

• \(G_t= 3\)

• 现在可以计算新的 \(V(S_0)\):

  

• (V(S_0) = V(S_0) + lr * [G_t — V(S_0)])

• (V(S_0) = 0 + 0.1 * [3 – 0])

• (V(S_0) = 0.3)

  

时序差分算法：在每一步进行学习

另一方面，时序差分学习只需要一次交互（一步）S{t+1}，就可以形成一个TD目标，并使用 R{t+1} 和 γ*V(S_{t+1}) 更新 V(S_t)。

TD算法的思想是在每一步都对 V(S_t) 进行更新。

但是因为我们没有经历整个回合，所以我们没有 (G_t)（期望回报）。相反，我们通过添加 (R_{t+1}) 和下一个状态的折扣值来估计 (G_t)。

这被称为自举（bootstrapping），因为时序差分方法的更新部分是基于现有估值 V(S_{t+1}) 而不是完整样本 (G_t)。

这种方法称为TD(0)或单步TD（在任何单个步骤后更新值函数）。

我们还是以猫和老鼠为例:

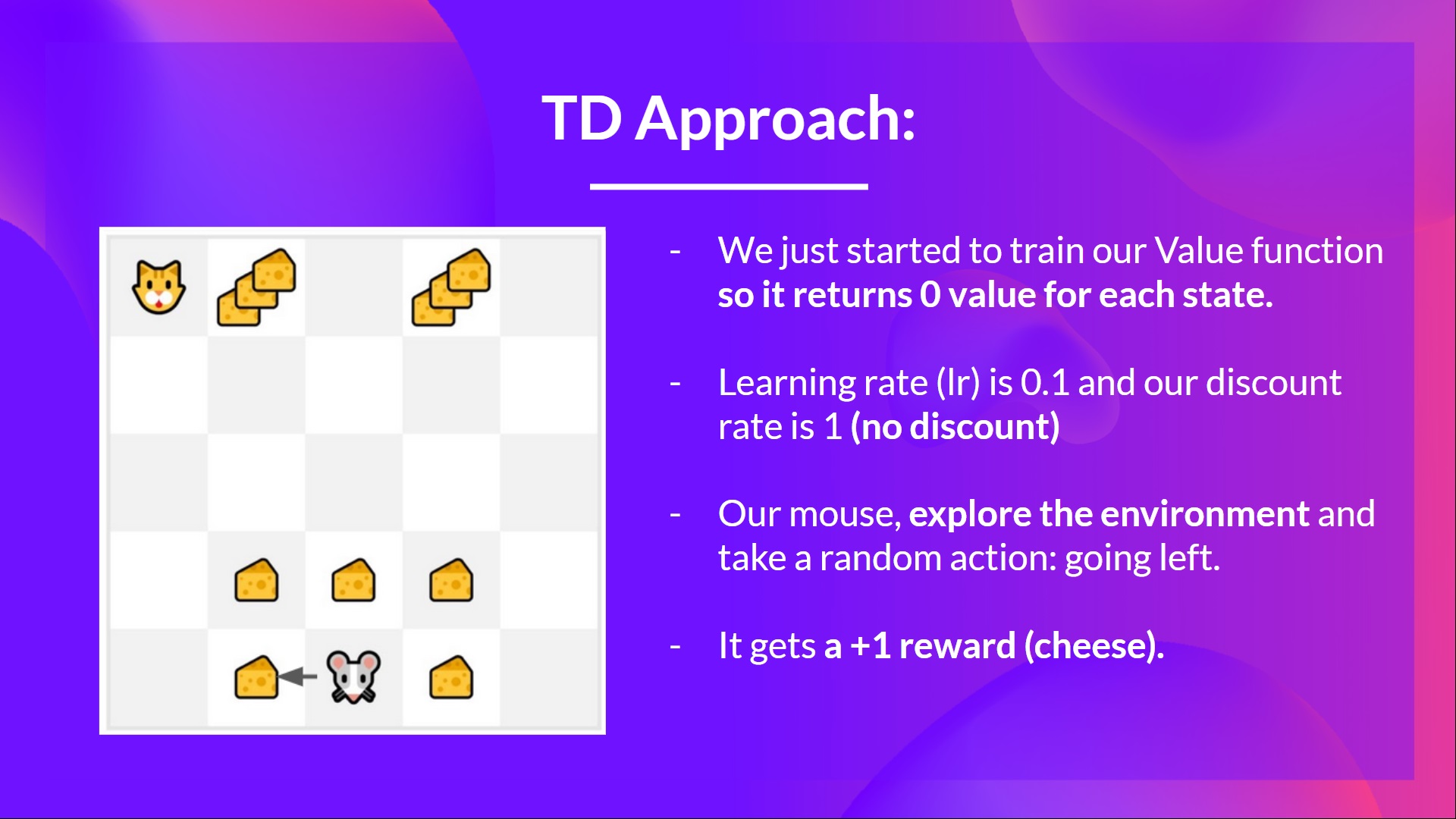
• 我们刚刚开始训练我们的价值函数，所以在每个状态都返回0值。

• 我们的学习率是0.1，并且折扣率为1（没有折扣）。

• 小老鼠探索环境并采取随机行为：向左移动

• 他得到了一个奖励 R_{t+1} = 1，因为它吃到了一块芝士

  

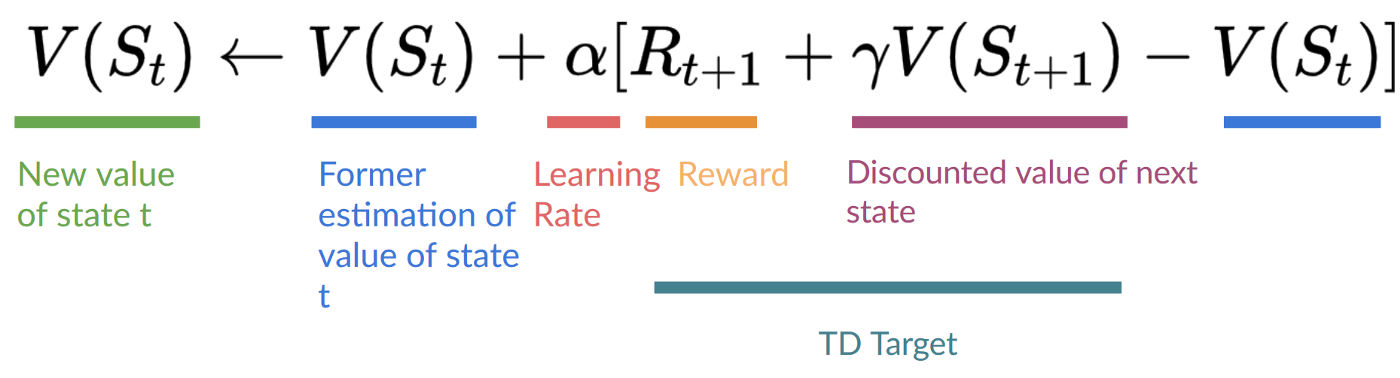
现在我们更新V(S_0)

新 (V(S_0) = V(S_0) + lr * [R_1 + \gamma * V(S_1) - V(S_0)])

新 (V(S_0) = 0 + 0.1 * [1 + 1 * 0–0])

新 (V(S_0) = 0.1)

所以我们从状态0开始更新我们的价值函数。

现在我们持续与这个环境进行交互，并更新价值函数。

总结一下：

• 在蒙特卡洛算法中，我们从完整的回合中更新价值函数，并使用本回合中确定的折扣回报。
• 在时序差分算法中，我们在每一步都对价值函数进行更新，所以我们将还没有获得的 (G_t) 替换为估计的回报，即TD-target。