2.3_贝尔曼方程_简化价值计算

贝尔曼方程简化了状态价值或状态-动作价值的计算。

根据现在所学的，我们知道如果计算 V(S_t) (状态的价值)，那么需要计算在该状态开始并在之后一直遵循该策略的回报。（我们在下面的例子中定义的策略是一个贪心策略；简单起见，我们没有对奖励进行折扣计算）

所以为了计算 V(S_t) ，我们需要计算期望回报的总和。因此：

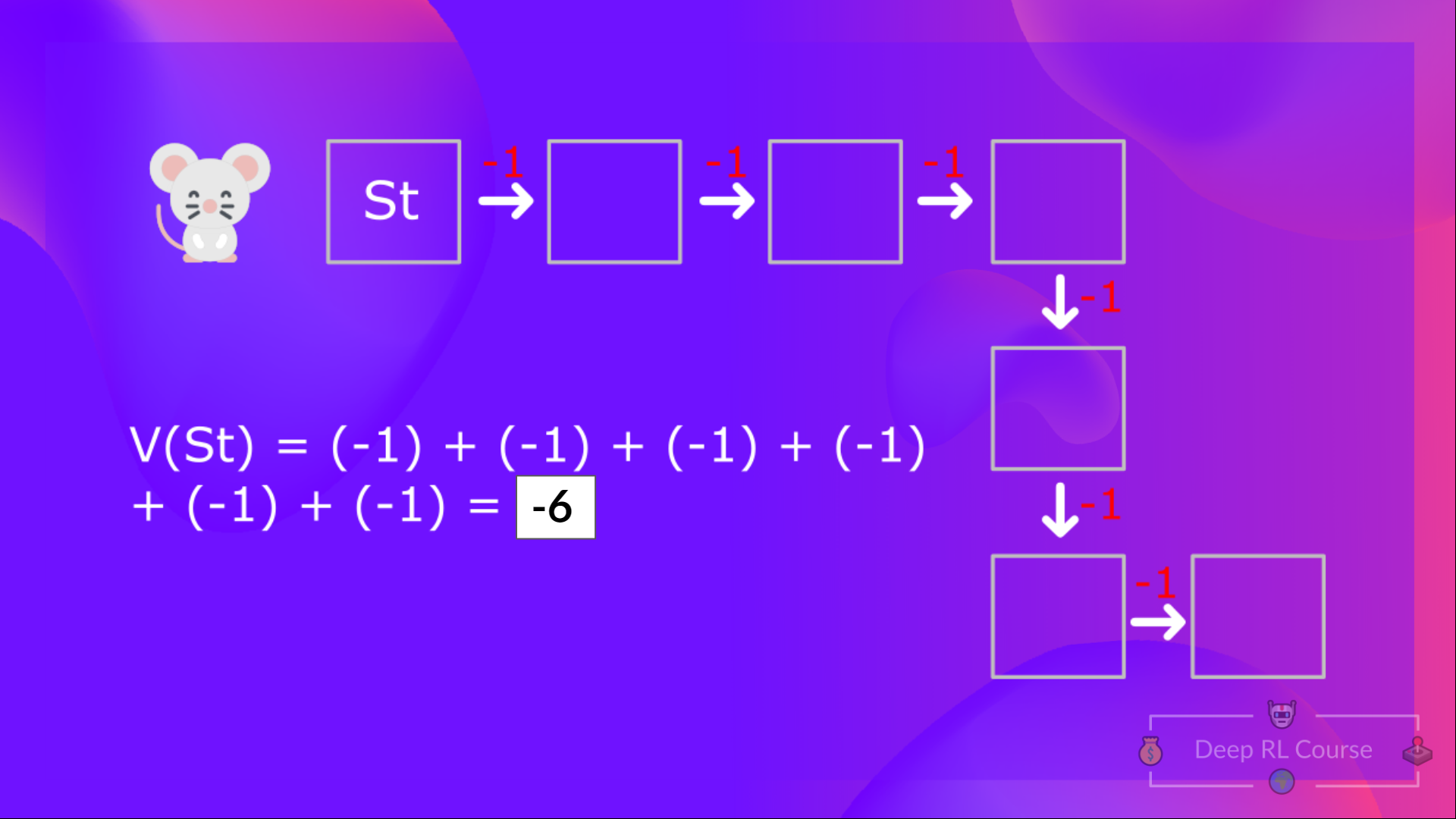
为了计算 （V(S{t+1}) ，我们需要计算在该状态 S{t+1} 的回报。

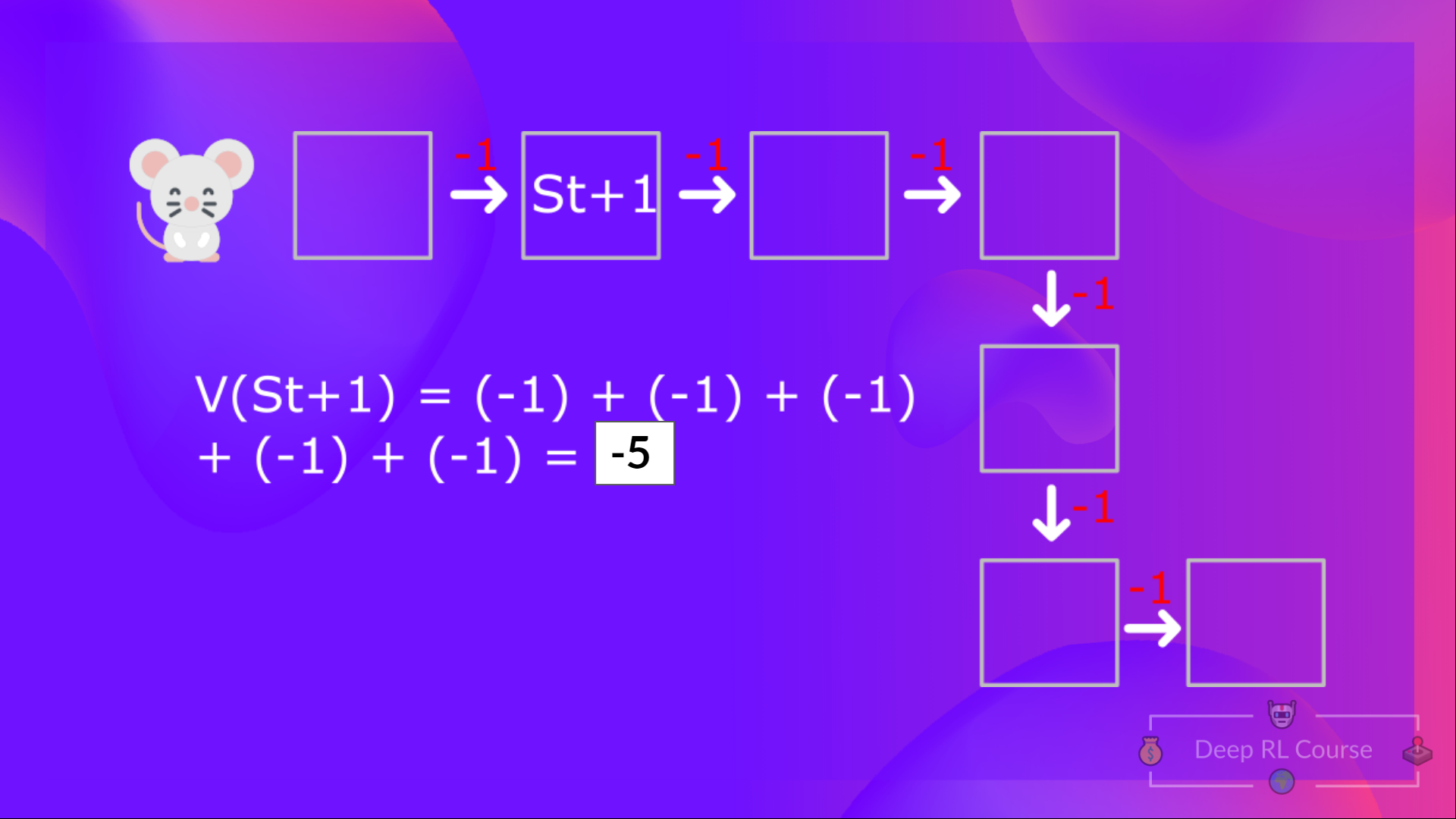
所以我们用贝尔曼方程来代替对每一个状态或每一个状态动作对求预期回报。（提示：这和动态规划很类似）

贝尔曼方程是一个递归方程，其大致是这样的：与其从头开始计算每个状态的回报，我们不如将所有状态的价值描述为：

即时奖励 (R{t+1}) + 状态的折扣价值 (gamma * V(S_{t+1}) )

如果我们回顾之前的例子，我们可以认为如果从状态 1 开始行动，那么状态 1 的价值和期望累计回报相等。

计算状态 1 的价值：如果智能体从状态 1 开始行动，并一直在之后的时间步中遵循该策略，则把每一步的奖励进行加和。

这用公式表示出来就是：V(S{t}) = 即时奖励 R{t+1} + 下个状态的折扣价值 gamma * V(S_{t+1})

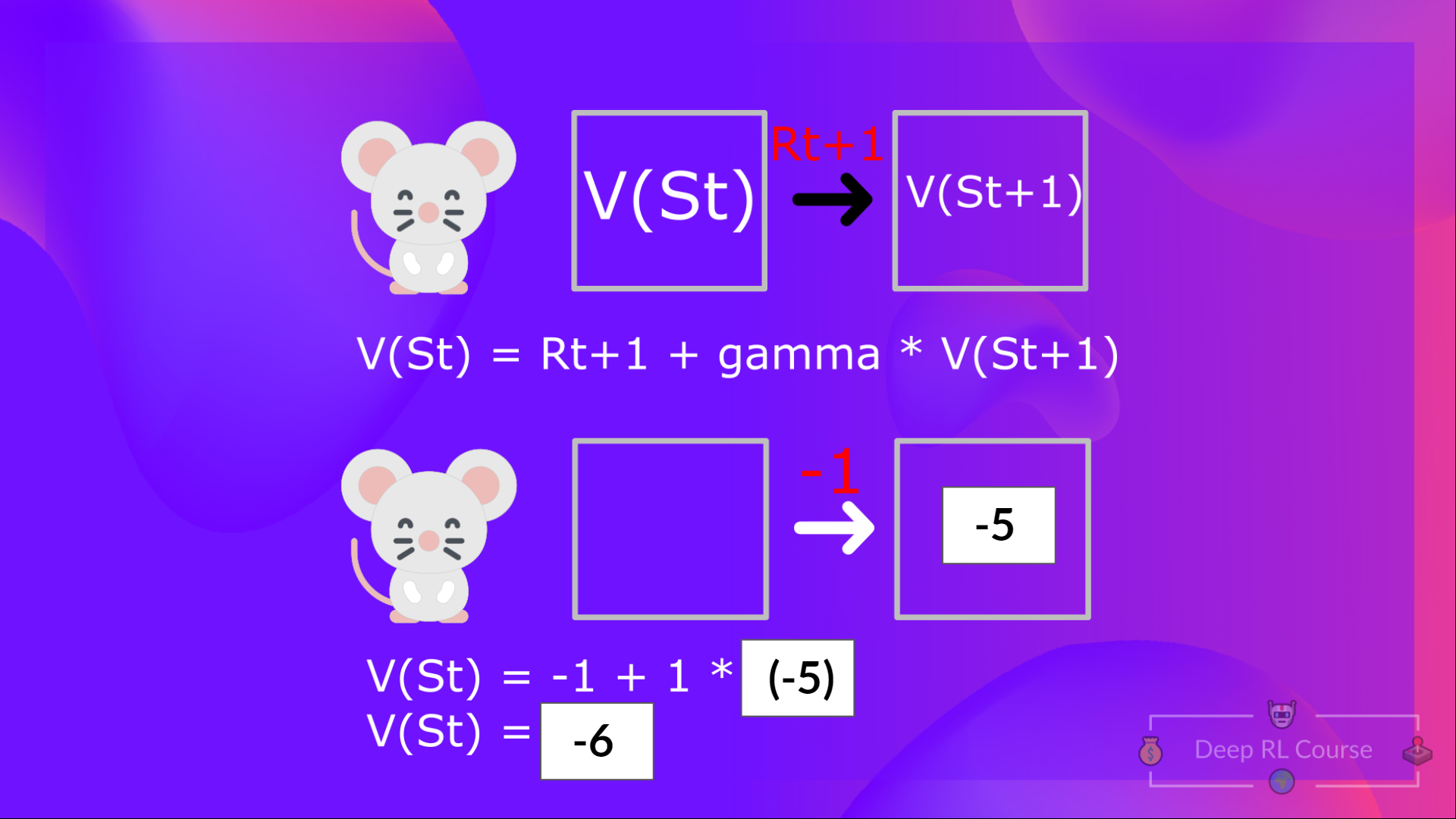
但是你将在本单元的Q-learning部分学到一个gamma = 0.99的例子：

• V(S{t+1}) = 即时奖励 (R{t+2}) + 下一个状态的折扣价值 (gamma * V(S_{t+2})
• 诸如此类

现在我们将内容进行回顾，相较于繁琐的计算每一个价值，然后最终加和作为预期回报，贝尔曼方程的思想则是对即时的奖励以及之后状态的折扣价值进行加和从而得到期望回报。

在进入下一节课程前，让我们先思考一下贝尔曼方程中的折扣因子gamma的作用。如果gamma的值非常小会发生什么，如果为1会发生什么？或者gamma非常大，假如是一百万，又会发生什么？